THƯỢNG ĐẾ VÀ CÁI VÔ HẠN – KHÁT VỌNG TỚI CÁI VÔ HẠN

Archimedes và phép tính số π

Vô hạn “tiềm tàng” còn biểu hiện dưới những dạng khác nữa. Ví dụ, hãy xét một con số kì lạ mà ta biểu diễn bằng ký hiệu π, con số mà từ thủa sơ khai đã kích thích trí tò mò không chỉ các nhà toán học mà cả những kẻ ngoại đạo nữa. Chúng ta đều biết rằng π là tỉ số giữa chu vi của 1 vòng tròn với đường kính của nó. Bằng các đo đạc thực nghiệm chu vi và đường kính của các đường tròn, người xưa đã biết rằng tỉ số này xấp xỉ bằng 3. Nhưng người Hi Lạp là những người đầu tiên đề xuất ra phương pháp toán học chặt chẽ để tính, chứ không phải đơn giản chỉ bằng cách đo đạc, giá trị của π. Khi làm điều này, họ lại một lần nữa đối mặt với vô hạn.

Nhà toán học Archimedes (287-212 tr. CN) ở thành phố Syracuse, nổi tiếng với những nghiên cứu về các vật nổi (và chính ông là người đã thét lên Eureka! lúc đang ở trong bồn tắm khi ông phát hiện ra “lực đẩy” ngày nay mang tên ông, lực cho phép những vật có khối lượng riêng nhỏ hơn nước nổi lên) là người đã nghĩ ra phương pháp này. Hãy lấy một vòng tròn, ông giải thích, và tưởng tượng một đa giác đều nội tiếp vòng tròn đó, tức là tất cả các đỉnh của nó đều nằm trên vòng tròn và tất cả các cạnh và các góc của nó đều bằng nhau. Đa giác này có chu vi nhỏ hơn chu vi đường tròn. Nhưng khi ta càng tăng dần số cạnh của đa giác, đa giác này sẽ càng sát với đường tròn, và chu vi của đa giác sẽ tiến tới chu vi của đường tròn. Sau đó chỉ cần đo chu vi của đa giác rồi chia cho đường kính của hình tròn để nhận được giá trị của π hơi nhỏ hơn một chút so với giá trị thực. Lặp lại quá trình trên nhưng lần này đa giác không phải là nội tiếp mà là ngoại tiếp với vòng tròn. Vòng tròn lần này nằm trong đa giác và các cạnh của đa giác tiếp xúc với đường tròn. Một lần nữa hãy làm tăng số cạnh của đa giác: và như lần trước đa giác sẽ ngày càng tiến sát tới vòng tròn. Lần này, khi ta chia chu vi của đa giác cho đường kính của vòng tròn, ta sẽ thu được một giá trị hơi lớn hơn giá trị thực của π (hình dưới).

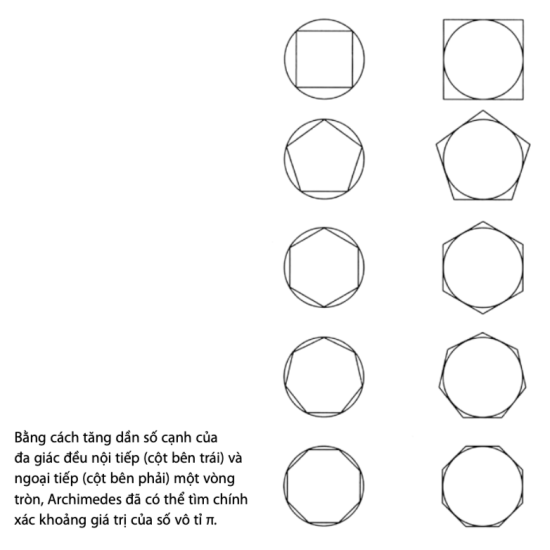
Bằng cách sử dụng một đa giác đều 96 cạnh mà ông biết rõ cách tính chu vi, Archimedes thu được giá trị thực của π phải nằm trong khoảng 3,14103 và 3,14271. Một sự gần đúng đáng kinh ngạc bởi vì giá trị thực của π như ta biết là 3,14159…

Nhưng ta cần phải hiểu rõ cái mới và mang tính cách mạng ở đây không phải là việc Archimedes đã có thể ước lượng được giá trị của π với độ chính xác cao hơn nhiều so với người đi trước mà chính là việc ông đã nghĩ ra phương pháp cho phép tính toán con số này với một độ chính xác lớn tùy ý, đơn giản chỉ bằng cách cố gắng làm khớp hình tròn với hình đa giác có số cạnh có thể tăng lên vô hạn. Theo ngôn ngữ toán học hiện đại, ngôn ngữ của phép tính vi phân được phát minh vào thế kỷ 19, π là giới hạn của dãy các chu vi khi số cạnh của đa giác tiến tới vô hạn. Như vậy Archimedes đã sử dụng khái niệm vô hạn tiềm tàng để giải quyết một vấn đề cơ bản, đó là việc tính số π.

Thượng đế và cái vô hạn

Trong hơn 2000 năm tiếp nối kỷ nguyên vàng của tư tưởng Hi Lạp, có rất ít phát hiện mới liên quan tới khái niệm vô hạn. Nhưng vẫn xảy ra những sự kiện lớn. Hi Lạp trở thành thuộc địa của Đế chế La Mã vào cuối thế kỷ thứ 2 tr. CN. Sự chói lọi của tư tưởng Hi Lạp tàn dần trong thời kỳ này. Người La Mã chẳng mấy quan tâm tới những tư biện trừu tượng. Các cuộc xâm chiếm không ngừng của các dân tộc hoang dã, Goths và Huns, từ phía đông vào thế kỷ thứ 5 và 6 đã giáng đòn quyết định vào Đế chế La Mã đang suy yếu vì suy thoái chính trị và hỗn loạn kinh tế. Tri thức Hi Lạp biến mất ở phương Tây.

Song song với sự sụp đổ của Đế chế La Mã, đã nổi lên Đế chế A rập trải dài từ Tây Ban Nha tới Ấn Độ. Ngọn đuốc văn minh và khoa học được sang tay các khalip của Bagdad. Ngay từ năm 1000, Tây Ban Nha đã trở thành trung tâm trí tuệ lớn của thế giới hồi giáo và qua nó, châu Âu thiên chúa giáo tái phát hiện lại tư tưởng Hi Lạp. Khái niệm về vô hạn lại nổi trở lại vào thời Trung Cổ, nhưng trong một bối cảnh mới: bối cảnh tôn giáo.

Cuộc kiếm tìm cái vô hạn thường gắn với một nghiên cứu về sự siêu việt, về những cái vượt ra khỏi kinh nghiệm thông thường, vượt ra ngoài những gì được nhìn thấy hay cảm nhận thấy trong cuộc sống hằng ngày. Sự siêu việt này thường được gắn với Thượng Đế, và Vô hạn chính là một trong những thuộc tính quan trọng của Thượng Đế. Và khi đó, một câu hỏi được đặt ra là: nếu như Thượng Đế là vô hạn, liệu Ngài có thể tạo ra vô hạn hiện thực hay cũng như con người, Ngài vẫn bị giới hạn bởi vô hạn tiềm tàng?

Lại xét dãy các số nguyên. Do không có kết thúc trong tiến trình liệt kê và không tồn tại một số nguyên nào lớn hơn tất cả các số còn lại, chúng ta không thể nói tới một tổng của toàn bộ các số nguyên: một lần nữa, vô hạn chỉ là tiềm tàng chứ không phải là hiện thực. Nhưng với Thượng Đế thì sao? Liệu Ngài có thể đạt được tới cái vô hạn hiện thực, hay cũng có giới hạn đối với tri thức của Ngài?

Thánh Augustin (354 – 430) đã đưa ra một câu trả lời chắc nịch cho các vấn đề này: “Đúng là có vô hạn các con số. Nhưng liệu có phải vì chúng là vô hạn mà Thượng Đế không thể biết hết?… Không ai có thể điên rồ tới mức đưa ra một điều sai sự thực như thế… Không còn nghi ngờ gì nữa, Ngài đều biết tới từng con số một. Với Thượng Đế, vô hạn trở nên hữu hạn bởi không thể có gì vượt ra khỏi tri thức của Ngài.” Với trí tuệ thần thánh, vô hạn trở nên hữu hạn và với Thượng Đế, vô hạn không còn là tiềm tàng nữa mà là hiện thực.

Vào thời Trung Cổ, thánh Thomas d’Aquin (1225-1274) sử dụng lập luận xâu chuỗi các nguyên nhân để chứng tỏ sự tồn tại thánh thần: mọi thứ đều có nguyên nhân, nhưng không thể có một chuỗi vô hạn các nguyên nhân được. Điều đó có nghĩa là sớm hay muộn ta phải tới được nguyên nhân đầu tiên, tức nguyên nhân của mọi thành phần trong vũ trụ. Nguyên nhân đầu tiên này chính là Thượng Đế. Theo thánh Thomas d’Aquin, chỉ một đấng vô hạn như Thượng Đế mới có thể nghĩ tới vô hạn hiện thực. Bất cứ ai nhăm nhe lĩnh hội cái vô hạn cũng sẽ mắc tội kiêu ngạo.

Còn hồng y người Đức Nicolas de Cues (1401-1464), người đã nghiên cứu toán học cổ đại, đã so sánh tri thức của Thượng Đế với vòng tròn và tri thức của con người giống như đa giác nội tiếp trong vòng tròn đó. Sử dụng lại suy luận của Archimedes, ông đã đưa ra một lập luận, theo đó tri thức của con người ngày càng tăng, số cạnh của đa giác cũng tăng lên và tiến tới vô hạn. Nhưng tri thức của con người sẽ không bao giờ bằng được với Thượng Đế, giống như đa giác nội tiếp không bao giờ có thể trở thành vòng tròn được, ngay cả khi số cạnh của nó tiến đến vô hạn.

Trong vũ trụ học, Nicolas de Cues là người bảo vệ ý tưởng về một vũ trụ vô hạn trong chuyên luận De la docte ignorance (1440) của ông, bởi vì Thượng Đế không thể bị giới hạn trong các tác phẩm của Người: “Nguyên lý đủ đầy” ngầm định rằng thế giới mà Ngài tạo ra không có giới hạn.